Phương trình mặt cầu là nội dung quan trọng trong hình học không gian lớp 12 và thường xuất hiện trong các đề thi THPTQG. Bài viết này sẽ giúp bạn nắm vững lý thuyết, cách lập phương trình mặt cầu và các dạng bài tập cơ bản, đồng thời khám phá ứng dụng thực tiễn trong không gian ba chiều. Cùng Phuongtrinhmatcau ôn tập và chinh phục dạng toán này một cách dễ dàng!
1. Mặt cầu là gì?
Mặt cầu trong không gian ba chiều được định nghĩa là tập hợp tất cả các điểm cách đều một điểm cố định một khoảng cố định. Trong đó:
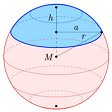
- Tâm cầu: Là điểm cố định \( M(x_0, y_0, z_0) \).
- Bán kính: Là khoảng cách từ tâm cầu đến bất kỳ điểm nào trên mặt cầu, ký hiệu là \( R > 0 \).
Phương trình mặt cầu được thiết lập dựa trên định nghĩa về khoảng cách giữa hai điểm trong không gian ba chiều.
2. Phương trình tổng quát của mặt cầu
Phương trình mặt cầu có dạng tổng quát như sau: $ (x – x_0)^2 + (y – y_0)^2 + (z – z_0)^2 = R^2, $ trong đó:
- \( (x_0, y_0, z_0) \): Tọa độ tâm cầu.
- \( R \): Bán kính của mặt cầu.
Ý nghĩa:
- Bất kỳ điểm \( M(x, y, z) \) nào thỏa mãn phương trình này đều nằm trên mặt cầu.
- Ngược lại, nếu một điểm \( M(x, y, z) \) nằm trên mặt cầu, khoảng cách từ điểm đó đến tâm cầu \( O \) luôn bằng bán kính \( R \).
3. Các dạng khác của phương trình mặt cầu
Phương trình chính tắc của mặt cầu
Phương trình chính tắc là dạng chuẩn của phương trình mặt cầu: $ (x – x_0)^2 + (y – y_0)^2 + (z – z_0)^2 = R^2. $
Dạng này thường được sử dụng khi tọa độ tâm \( (x_0, y_0, z_0) \) và bán kính \( R \) đã được xác định rõ ràng.
Phương trình mặt cầu khi khai triển
Khai triển phương trình chính tắc, ta được dạng đầy đủ: $ x^2 + y^2 + z^2 – 2x_0x – 2y_0y – 2z_0z + x_0^2 + y_0^2 + z_0^2 – R^2 = 0. $
Dạng này thường viết gọn thành: $ x^2 + y^2 + z^2 + Ax + By + Cz + D = 0, $ với:
– \( A = -2x_0, B = -2y_0, C = -2z_0, D = x_0^2 + y_0^2 + z_0^2 – R^2 \).
Nhận xét:
- Dạng này hữu ích khi cần xác định tâm và bán kính từ phương trình đã cho.
- Đây là dạng phổ biến khi phương trình mặt cầu xuất hiện trong các bài toán cần khai triển hoặc rút gọn.
4. Xác định tâm và bán kính từ phương trình mặt cầu
Khi phương trình mặt cầu có dạng: $ x^2 + y^2 + z^2 + Ax + By + Cz + D = 0, $
ta có thể xác định tâm và bán kính như sau:
- Tâm cầu: $ (x_0, y_0, z_0) = \left(-\frac{A}{2}, -\frac{B}{2}, -\frac{C}{2}\right). $
- Bán kính: $ R = \sqrt{x_0^2 + y_0^2 + z_0^2 – D}. $
Điều kiện: \( x_0^2 + y_0^2 + z_0^2 – D > 0 \) để \( R > 0 \).
Ví dụ: Cho phương trình mặt cầu: $ x^2 + y^2 + z^2 – 4x + 6y – 8z + 9 = 0. $
Xác định tâm và bán kính.
- Ta có: $ A = -4, B = 6, C = -8, D = 9. $
- Tâm cầu: $ (x_0, y_0, z_0) = \left(-\frac{-4}{2}, -\frac{6}{2}, -\frac{-8}{2}\right) = (2, -3, 4). $
- Bán kính: $R = \sqrt {x_0^2 + y_0^2 + z_0^2 – D} $ $ = \sqrt {{2^2} + {{( – 3)}^2} + {4^2} – 9} $ $ = \sqrt {4 + 9 + 16 – 9} $ $ = \sqrt {20} .$
Vậy, tâm cầu là \( (2, -3, 4) \) và bán kính là \( \sqrt{20} \).
5. Một số bài toán liên quan đến phương trình mặt cầu
Lập phương trình mặt cầu
Bài toán: Lập phương trình mặt cầu có tâm \( O(1, 2, 3) \) và bán kính \( R = 5 \).
Lời giải
Sử dụng phương trình chính tắc: $ (x – x_0)^2 + (y – y_0)^2 + (z – z_0)^2 = R^2. $
Thay \( x_0 = 1, y_0 = 2, z_0 = 3, R = 5 \), ta được: $ (x – 1)^2 + (y – 2)^2 + (z – 3)^2 = 25. $
Xác định vị trí của điểm đối với mặt cầu
Bài toán: Cho mặt cầu: $ x^2 + y^2 + z^2 – 2x + 4y – 6z – 20 = 0. $ Xác định vị trí điểm \( M(2, -1, 3) \) so với mặt cầu.
Lời giải
Xác định tâm và bán kính:
- Tâm cầu \( (x_0, y_0, z_0) = (1, -2, 3) \).
- Bán kính: $R = \sqrt {x_0^2 + y_0^2 + z_0^2 – D} $ $ = \sqrt {{1^2} + {{( – 2)}^2} + {3^2} – ( – 20)} $ $ = \sqrt {30} .$
- Tính khoảng cách từ \( M(2, -1, 3) \) đến tâm \( O(1, -2, 3) \): $d = \sqrt {{{(2 – 1)}^2} + {{( – 1 – ( – 2))}^2} + {{(3 – 3)}^2}} $ $ = \sqrt {{1^2} + {1^2} + {0^2}} = \sqrt 2 .$
So sánh:
- Nếu \( d < R \): Điểm nằm trong mặt cầu.
- Nếu \( d = R \): Điểm nằm trên mặt cầu.
- Nếu \( d > R \): Điểm nằm ngoài mặt cầu.
Ở đây, \( d = \sqrt{2} < R = \sqrt{30} \), nên \( M \) nằm trong mặt cầu.
6. Một số dạng bài toán mở rộng
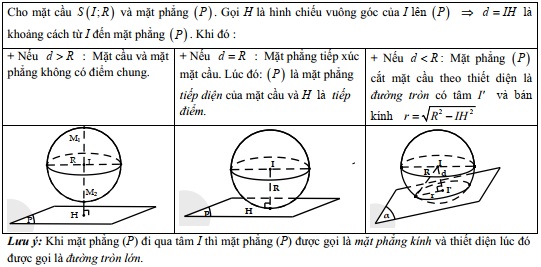
6.1 Giao của mặt cầu và mặt phẳng
Khi một mặt cầu cắt mặt phẳng, giao tuyến của chúng là một đường tròn. Để xác định phương trình giao tuyến:
- Thay phương trình mặt phẳng vào phương trình mặt cầu.
- Phương trình thu được là phương trình đường tròn trong không gian.
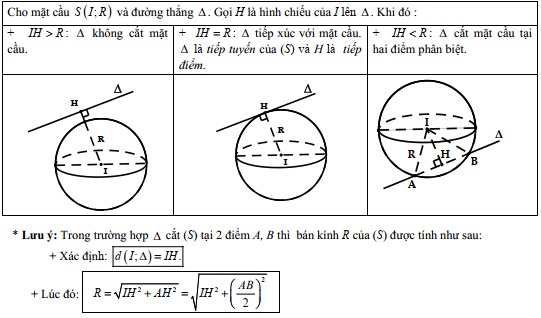
6.2 Vị trí tương đối giữa mặt cầu và đường thẳng
6.3 Giao của hai mặt cầu
Khi hai mặt cầu giao nhau, giao tuyến của chúng là một đường tròn (nếu chúng không tiếp xúc). Để tìm giao tuyến:
- Lấy hệ phương trình của hai mặt cầu.
- Loại bỏ một biến để thu được phương trình mặt phẳng chứa giao tuyến.
7. Bài tập vận dụng
Bài tập 1. Tìm tâm và bán kính của các mặt cầu có phương trình sau đây:
a) \({x^2} + {(y – 3)^2} + {(z + 2)^2} = 1\)
b) \({(x – 2)^2} + {(y – 3)^2} + {z^2} = 4\)
c) \({x^2} + {y^2} + {z^2} – 8x – 2y + 1 = 0\)
d) \(3{x^2} + 3{y^2} + 3{z^2} – 6x + 8y + 15z – 3 = 0\)
Lời giải
a) \({x^2} + {(y – 3)^2} + {(z + 2)^2} = 1\)
Từ phương trình, ta có:
– Tâm \(I(0,3, – 2)\)
– Bán kính \(R = \sqrt 1 = 1\)
b) \({(x – 2)^2} + {(y – 3)^2} + {z^2} = 4\)
Từ phương trình, ta có:
– Tâm \(I(2,3,0)\)
– Bán kính \(R = \sqrt 4 = 2\)
c) \({x^2} + {y^2} + {z^2} – 8x – 2y + 1 = 0\)
Ta có: \(({x^2} – 8x) + ({y^2} – 2y) + {z^2} = – 1\)
– \(x\): \({x^2} – 8x = {(x – 4)^2} – 16\)
– \(y\): \({y^2} – 2y = {(y – 1)^2} – 1\)
– Phương trình trở thành:
\({(x – 4)^2} + {(y – 1)^2} + {z^2} = 16 + 1 – 1 = 16\)
– Tâm \(I(4,1,0)\)
– Bán kính \(R = \sqrt {16} = 4\)
d) \(3{x^2} + 3{y^2} + 3{z^2} – 6x + 8y + 15z – 3 = 0\)
Chia cả hai vế cho 3: \({x^2} + {y^2} + {z^2} – 2x + \frac{8}{3}y + 5z = 1\)
– \(x\): \({x^2} – 2x = {(x – 1)^2} – 1\)
-\(y\): \({y^2} + \frac{8}{3}y = {\left( {y + \frac{4}{3}} \right)^2} – \frac{{16}}{9}\)
– \(z\): \({z^2} + 5z = {\left( {z + \frac{5}{2}} \right)^2} – \frac{{25}}{4}\)
– Phương trình trở thành: ${(x – 1)^2} + {\left( {y + \frac{4}{3}} \right)^2} + {\left( {z + \frac{5}{2}} \right)^2}$ $ = 1 + 1 + \frac{{16}}{9} + \frac{{25}}{4}$ $ = \frac{{79}}{{36}}$
– Tâm \(I\left( {1, – \frac{4}{3}, – \frac{5}{2}} \right)\)
– Bán kính \(R = \sqrt {\frac{{79}}{{36}}} = \frac{{\sqrt {79} }}{6}\)
Bài tập 2. Viết phương trình mặt cầu trong các trường hợp sau đây:
a) Có tâm \(I( – 4;0;5)\) và bán kính \(r = \sqrt 6 \);
b) Đi qua điểm \(A(5; – 2; – 1)\) và có tâm \(C(2;1;5)\);
c) Có đường kính AB với \(A( – 4;3;7)\) và \(B(2;1; – 3)\).
Lời giải
a) Tâm \(I( – 4;0;5)\) và bán kính \(r = \sqrt 6 \). Phương trình mặt cầu là:
\({(x + 4)^2} + {y^2} + {(z – 5)^2} = 6\)
b) Đi qua điểm \(A(5; – 2; – 1)\) và có tâm \(C(2;1;5)\). – Tính bán kính \(R = CA\):
$R = \sqrt {{{(5 – 2)}^2} + {{( – 2 – 1)}^2} + {{( – 1 – 5)}^2}} $ $ = \sqrt {{3^2} + {{( – 3)}^2} + {{( – 6)}^2}} $ $ = \sqrt {9 + 9 + 36} $ $ = \sqrt {54} $ $ = 3\sqrt 6 $
– Phương trình mặt cầu là:
\({(x – 2)^2} + {(y – 1)^2} + {(z – 5)^2} = 54\)
c) Có đường kính AB với \(A( – 4;3;7)\) và \(B(2;1; – 3)\).
– Tọa độ tâm \(I\) là trung điểm của AB:
\(I = \left( {\frac{{ – 4 + 2}}{2},\frac{{3 + 1}}{2},\frac{{7 – 3}}{2}} \right) = ( – 1,2,2)\)
– Bán kính \(R = \frac{1}{2}AB\):
$AB = \sqrt {{{(2 + 4)}^2} + {{(1 – 3)}^2} + {{( – 3 – 7)}^2}} $ $ = \sqrt {{6^2} + {{( – 2)}^2} + {{( – 10)}^2}} $ $ = \sqrt {36 + 4 + 100} $ $ = \sqrt {140} $ $ = 2\sqrt {35} $
\(R = \frac{{2\sqrt {35} }}{2} = \sqrt {35} \)
– Phương trình mặt cầu là:
\({(x + 1)^2} + {(y – 2)^2} + {(z – 2)^2} = 35\)
Bài tập 3. Bạn Bình đố bạn Nam tìm được đường kính của quả bóng rổ, biết rằng nếu đặt quả bóng ở một góc căn phòng hình hộp chữ nhật, sao cho quả bóng chạm (tiếp xúc) với hai bức tường và nền nhà của căn phòng đó (khoảng cách từ tâm quả bóng đến hai bức tường và nền nhà đều bằng bán kính của quả bóng) thì có một điểm M trên quả bóng với khoảng cách lần lượt đến hai bức tường và nền nhà là 17 cm, 18 cm và 21 cm.
Hãy giúp Nam xác định đường kính của quả bóng rổ. Biết rằng loại bóng rổ tiêu chuẩn có đường kính từ 23 cm đến 24,5 cm.
Lời giải
Đặt toạ độ O tại vị trí giao nhau giữa hai bức tường và nền nhà.
Toạ độ tương ứng với điểm M là \((17;18;21)\)
Gọi \(I(x;y;z)\) là tâm của quả bóng.
Vì khoảng cách từ tâm quả bóng đến hai bức tường và nền nhà đều bằng bán kính của quả bóng nên ta có: \(r = x = y = z\)
Suy ra I có toạ độ là \(I(r;r;r)\)
Do M nằm trên bề mặt quả bóng nên khoảng cách từ tâm I của quả bóng tới M chính là bán kính r, nên:
\(\begin{array}{l}\sqrt {{{(r – 17)}^2} + {{(r – 18)}^2} + {{(r – 21)}^2}} = r\\ \Leftrightarrow {r^2} – 34r + 289 + {r^2} – 36r + 324 + {r^2} – 42r + 441 = {r^2}\\ \Leftrightarrow 2{r^2} – 112r + 1054 = 0\end{array}\)
Từ phương trình trên ta thu được hai giá trị \({r_1} \approx 44,03\)và \({r_2} \approx 11,97\).
Vì loại bóng rổ tiêu chuẩn có đường kính từ 23 cm đến 24,5 cm nên ta loại giá trị \({r_1}\) và nhận giá trị \({r_2}\) làm bán kính của quả bóng.
Vậy đường kính của bóng rổ là 23,94 cm.
Bài tập 4. Cho hai điểm \(A\left( {1;0;0} \right)\) và \(B\left( {5;0;0} \right)\). Chứng minh rằng nếu điểm \(M\left( {x;y;z} \right)\) thoả mãn \(\overrightarrow {MA} .\overrightarrow {MB} = 0\) thì \(M\) thuộc một mặt cầu \(\left( S \right)\). Tìm tâm và bán kính của \(\left( S \right)\).
Lời giải
Ta có \(\overrightarrow {MA} = \left( {1 – x;y;z} \right)\) và \(\overrightarrow {MB} = \left( {5 – x;y;z} \right)\).
Do \(\overrightarrow {MA} .\overrightarrow {MB} = 0\) nên
\(\begin{array}{l}\left( {1 – x} \right)\left( {5 – x} \right) + {y^2} + {z^2} = 0\\ \Rightarrow {x^2} – 6x + 5 + {y^2} + {z^2} = 0\\ \Rightarrow \left( {{x^2} – 6x + 9} \right) + {y^2} + {z^2} = 4\\ \Rightarrow {\left( {x – 3} \right)^2} + {y^2} + {z^2} = 4\end{array}\)
Vậy điểm \(M\left( {x;y;z} \right)\) thuộc mặt cầu \(S\) có tâm \(I\left( {3;0;0} \right)\) và bán kính \(R = \sqrt 4 = 2\).
Bài tập 5. Người ta muốn thiết kế một bồn chứa khí hoá lỏng hình cầu bằng phần mềm 3D. Cho biết phương trình bề mặt của bồn chứa là \(\left( S \right):{\left( {x – 6} \right)^2} + {\left( {y – 6} \right)^2} + {\left( {z – 6} \right)^2} = 25\). Phương trình mặt phẳng chứa nắp là \(\left( P \right):z = 10\).
a) Tìm tâm và bán kính của bồn chứa.
b) Tính khoảng cách từ tâm bồn chứa đến mặt phẳng của nắp.
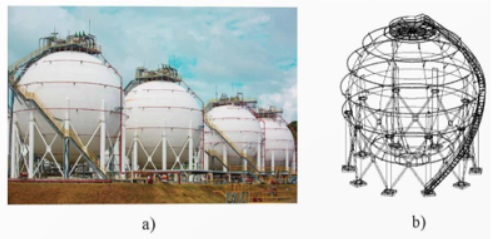
Lời giải
a) Phương trình bề mặt bồn chứa là \(\left( S \right):{\left( {x – 6} \right)^2} + {\left( {y – 6} \right)^2} + {\left( {z – 6} \right)^2} = 25\), nên bồn chứa là một hình cầu có tâm \(I\left( {6;6;6} \right)\) và bán kính \(R = \sqrt {25} = 5\).
b) Khoảng cách từ tâm bồn chứa \(I\left( {6;6;6} \right)\) đến mặt phẳng chứa nắp \(\left( P \right):z – 10 = 0\) là \(d = \frac{{\left| {0.6 + 0.6 + 1.6 – 10} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} }} = 4\).
Bài tập 6. Hệ thống định vị toàn cầu (tên tiếng Anh là: Global Positioning System, viết tắt là GPS) là một hệ thống cho phép xác định chính xác vị trí của một vật thể trong không gian (Hình 42). Ta có thể mô phỏng cơ chế hoạt động của hệ thống GPS trong không gian như sau: Trong cùng một thời điểm, toạ độ của một điểm M trong không gian sẽ được xác định bởi bốn vệ tinh cho trước, trên mỗi vệ tinh có một máy thu tín hiệu. Bằng cách so sánh sự sai lệch về thời gian từ lúc tín hiệu được phát đi với thời gian nhận phản hồi tín hiệu đó, mỗi máy thu tín hiệu xác định được khoảng cách từ vệ tinh đến vị trí M cần tìm tọa độ. Như vậy, điểm M là giao điểm của bốn mặt cầu với tâm lần lượt là bốn vệ tinh đã cho.
Ta xét một ví dụ cụ thể như sau:
Trong không gian với hệ tọa độ Oxyz, cho bốn vệ tinh A(3; – 1; 6), B(1; 4; 8), C(7; 9; 6), D(7; – 15; 18). Tìm tọa độ của điểm M trong không gian biết khoảng cách từ các vệ tinh đến điểm M lần lượt là MA = 6, MB = 7, MC = 12, MD = 24.

Lời giải
Gọi M(x; y; z).
Ta có: \(MA = \sqrt {{{\left( {3 – x} \right)}^2} + {{\left( { – 1 – y} \right)}^2} + {{\left( {6 – z} \right)}^2}} = 6\);
\(MB = \sqrt {{{\left( {1 – x} \right)}^2} + {{\left( {4 – y} \right)}^2} + {{\left( {8 – z} \right)}^2}} = 7\);
\(MC = \sqrt {{{\left( {7 – x} \right)}^2} + {{\left( {9 – y} \right)}^2} + {{\left( {6 – z} \right)}^2}} = 12\);
\(MD = \sqrt {{{\left( {7 – x} \right)}^2} + {{\left( { – 15 – y} \right)}^2} + {{\left( {18 – z} \right)}^2}} = 24\).
Ta có hệ phương trình: \(\left\{ \begin{array}{l}{\left( {3 – x} \right)^2} + {\left( { – 1 – y} \right)^2} + {\left( {6 – z} \right)^2} = 36\left( 1 \right)\\{\left( {1 – x} \right)^2} + {\left( {4 – y} \right)^2} + {\left( {8 – z} \right)^2} = 49\left( 2 \right)\\{\left( {7 – x} \right)^2} + {\left( {9 – y} \right)^2} + {\left( {6 – z} \right)^2} = 144\left( 3 \right)\\{\left( {7 – x} \right)^2} + {\left( { – 15 – y} \right)^2} + {\left( {18 – z} \right)^2} = 576\left( 4 \right)\end{array} \right.\)
Trừ vế với vế của (3) và (1) ta có: \({\left( {7 – x} \right)^2} – {\left( {3 – x} \right)^2} + {\left( {9 – y} \right)^2} – {\left( { – 1 – y} \right)^2} = 144 – 36\)
\( \Leftrightarrow – 8x – 20y = – 12 \Leftrightarrow x = \frac{{3 – 5y}}{2}\left( 5 \right)\).
Trừ vế với vế của (4) và (3) ta có: \({\left( { – 15 – y} \right)^2} – {\left( {9 – y} \right)^2} + {\left( {18 – z} \right)^2} – {\left( {6 – z} \right)^2} = 576 – 144\)
\( \Leftrightarrow 48y – 24z = 0 \Leftrightarrow z = 2y\left( 6 \right)\).
Thay (5) và (6) vào (2) ta có: \({\left( {1 – \frac{{3 – 5y}}{2}} \right)^2} + {\left( {4 – y} \right)^2} + {\left( {8 – 2y} \right)^2} = 49\)
\( \Leftrightarrow 45{y^2} – 170y + 125 = 0 \Leftrightarrow y = 1\) hoặc \(y = \frac{{25}}{9}\).
+ Với \(y = 1\) ta có: \(x = – 1;z = 2\). Khi đó, M(-1; 1; 2). Thay tọa độ của M vào các phương trình (1), (2), (3), (4) ta thấy thỏa mãn.
+ Với \(y = \frac{{25}}{9}\) ta có: \(x = – \frac{{49}}{9};z = \frac{{50}}{9}\). Khi đó, \(M\left( {\frac{{ – 49}}{9};\frac{{25}}{9};\frac{{50}}{9}} \right)\). Thay tọa độ của M vào các phương trình (1) ta thấy không thỏa mãn.
Vậy điểm M(-1; 1; 2) thỏa mãn yêu cầu đề bài.
Bài tập 7. Lập phương trình mặt cầu (S) trong mỗi trường hợp sau:
a) (S) có tâm I(3; -7; 1) và bán kính \(R = 2\);
b) (S) có tâm I(-1; 4; -5) và đi qua điểm M(3; 1; 2);
c) (S) có đường kính là đoạn thẳng CD với C(1; -3; -1) và D(-3; 1; 2).
Lời giải
a) (S) có tâm I(3; -7; 1), bán kính \(R = 2\) có phương trình là \({\left( {x – 3} \right)^2} + {\left( {y + 7} \right)^2} + {\left( {z – 1} \right)^2} = 4\).
b) (S) có tâm I và bán kính \(IM = \sqrt {{{\left( {3 + 1} \right)}^2} + {{\left( {1 – 4} \right)}^2} + {{\left( {2 + 5} \right)}^2}} = \sqrt {74} \) nên phương trình mặt cầu (S) là: \({\left( {x + 1} \right)^2} + {\left( {y – 4} \right)^2} + {\left( {z + 5} \right)^2} = 74\).
c) Gọi I là trung điểm của CD nên \(I\left( { – 1; – 1;\frac{1}{2}} \right)\).
Vì mặt cầu (S) có đường kính là CD nên (S) có tâm \(I\left( { – 1; – 1;\frac{1}{2}} \right)\), bán kính
$R = IC$ $ = \sqrt {{{\left( {1 + 1} \right)}^2} + {{\left( { – 3 + 1} \right)}^2} + {{\left( { – 1 – \frac{1}{2}} \right)}^2}} $ $ = \frac{{\sqrt {41} }}{2}$
Do đó, phương trình mặt cầu (S) là: \({\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z – \frac{1}{2}} \right)^2} = \frac{{41}}{4}\).
Bài tập 8. Trong không gian Oxyz, viết phương trình của mặt cầu (S) có tâm \(I\left( {0;3; – 1} \right)\) và có bán kính bằng khoảng cách từ tâm I đến mặt phẳng \(\left( P \right):3x + 2y – z = 0\).
Lời giải
Ta có: \(d\left( {I;\left( P \right)} \right) = \frac{{\left| {3.0 + 2.3 – 1.\left( { – 1} \right)} \right|}}{{\sqrt {{3^2} + {2^2} + {{\left( { – 1} \right)}^2}} }} = \frac{7}{{\sqrt {14} }}\) nên bán kính của mặt cầu (S) là \(R = \frac{7}{{\sqrt {14} }}\).
Do đó, phương trình của mặt cầu (S) có tâm \(I\left( {0;3; – 1} \right)\) và có bán kính \(R = \frac{7}{{\sqrt {14} }}\) là: \({x^2} + {\left( {y – 3} \right)^2} + {\left( {z + 1} \right)^2} = \frac{7}{2}\)
Phương trình mặt cầu mô tả tập hợp các điểm cách đều một điểm cố định trong không gian ba chiều, giúp giải quyết các bài toán về tâm, bán kính, vị trí và giao tuyến. Với nhiều ứng dụng thực tiễn, việc nắm vững công cụ này giúp xử lý hiệu quả các bài toán không gian phức tạp.
